DC electrical resistivity surveying measures resistivity, a volumetric property, with units of resistance (ohms) * meters (m) or ohm-m (Ω m). In resistivity surveying, we introduce an electrical field into the subsurface at two points (current dipoles) and measure the resulting difference in electrical potential between two other surface points (potential dipoles). Where surface electrodes are used, this surveying is referred to as electrical resistivity imaging (ERI).
Subsurface resistivity varies widely because it is mainly influenced by porosity, amount and salinity of pore water, and clay and metallic mineral content which vary widely. Importantly, those variations coincide with fine-scale variations in geology and in site conditions. Unsaturated sediments above the water table have higher resistivities than saturated sediments below the water table. Organic deposits such as peat have relatively low resistivity because of their high water content. Bedrock commonly has higher resistivity than overlying, water-saturated sediments.
Think of the current applied in a resistivity survey traveling into the subsurface along current flowlines. These are distorted by the different resistivities of subsurface materials. The spatial pattern of the resulting potential differences measured at surface reflects the distribution of variable subsurface resistivity. Technically, the surface potential differences are converted into apparent resistivities. The subsurface resistivity distribution can be backed out of the apparent resistivity data and interpreted in terms of the geometry and types of geologic materials, water properties, even building materials and contaminants.
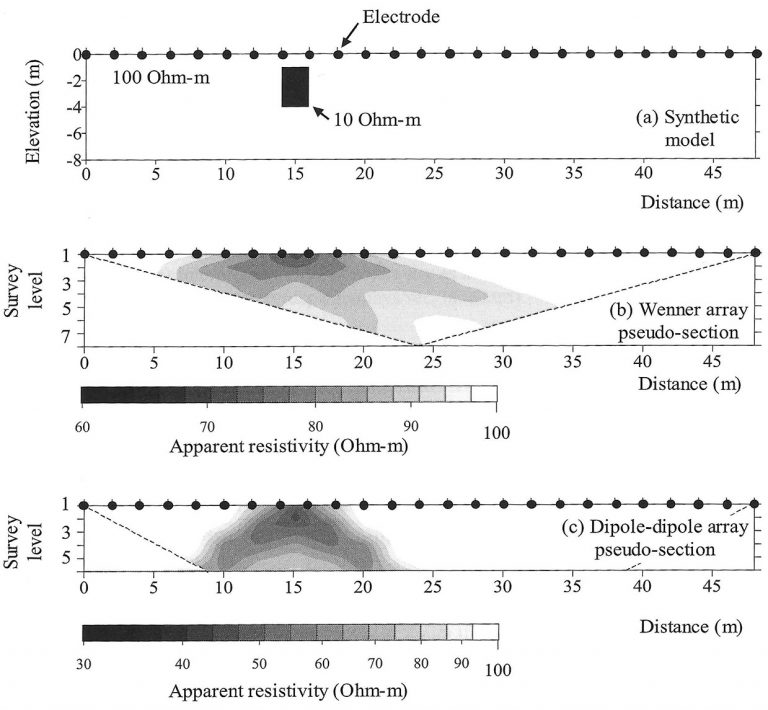
In a survey using a line of many, equally space electrodes (Fig. 1, black dots), one follows any of several protocols that specify a sequence of steps that each involve current injection at two electrodes and measurement of electrical potential at other electrodes. The measurement protocols, referred to as arrays (e.g., Wenner, Schlumberger, dipole-dipole arrays), produce a large number of individual measurements with distinct differences between the different arrays. The measurements, converted to apparent resistivity, are arranged in a pseudo-section (Fig.1). This is not a cross-section of subsurface resistivity; it is a plot of all measurements. Survey depth or level (y-axis) is increased by increasing the distance between current electrodes which increases the effective depth of the sensitivity of the survey.
Fig. 1. An example subsurface resistivity distribution (a) and two different pseudo-sections of apparent resistivity (b, c) produced by different measurement arrays. The example features a shallow pit (2.5 x 3 m) of conductive material (10 Ωm) in more resistive material. Electrode spacing is 2.5 m. The pseudo-section for the Wenner array smears the true resistivity distribution laterally (b). The pseudo-section for the Dipole-Dipole array smears the true resistivity distribution vertically and laterally. Source: Binley and Kemna, 2006.
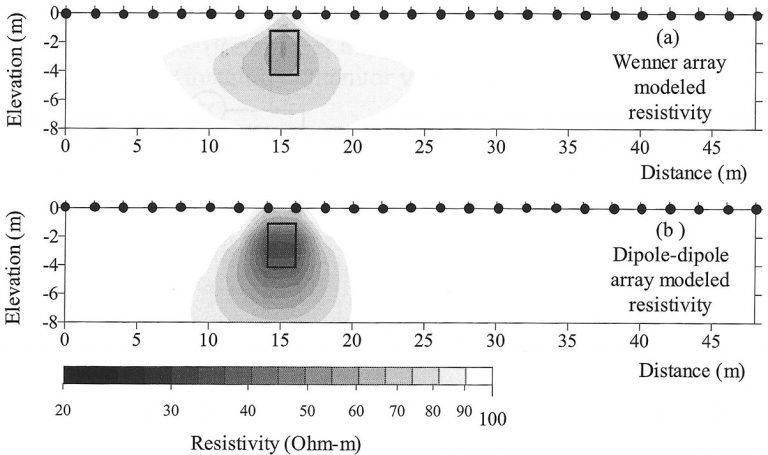
Apparent resistivities are converted to subsurface resistivity images by solving an inverse tomographic problem. The objective of inversion is to determine a subsurface resistivity model that explains the data. In the inversion, the data, namely, voltage normalized by current, apparent resistivity, and electrode geometry are inverted to obtain the subsurface resistivity distribution. An example of the different subsurface resistivity models that result from inverting the pseudo-sections in Fig. 1 are shown in Fig. 2. Note that the two subsurface resistivity models in Fig. 2 differ. This highlights the fact that solutions to the inverse problem are not unique. Therefore, inverse problems are solved as an optimization problem using techniques that generate a theoretical apparent resistivity section from a subsurface resistivity distribution that closely resembles the observed apparent resistivity section.
Fig. 2. Inverted subsurface resistivity models for the pseudo-sections in Fig. 1b, c. The position of the shallow pit with conductive material from Fig. 1a is shown. Each of these inverted resistivity models portray the true subsurface resistivity differently. Neither gives the exact boundary of the pit and they differ on the minimum resistivity of pit fill. This highlights the importance of using multiple measurement arrays and need for significant interpretation skill. Source: Binley and Kemna, 2006.
Penetration depth and spatial resolution of an electrical resistivity survey are crucial issues. Penetration depth is roughly 15-25% of the total length of the electrode array. Horizontal spatial resolution of the subsurface resistivity distribution is conservatively ~ 2x the electrode spacing near the surface which should provide two electrodes covering the target space. Some say that significant resistivity changes over ~ ½ x the electrode spacing are evident in resistivity profiles collected using certain arrays. Spatial resolution decreases with depth, resistivity contrast between target and surrounding material, target shape, and inversion methods. Thus, spatial resolution at maximum penetration depth is probably 2x to 4x the electrode spacing.
